FUEL CELL THERMODYNAMICS

The contents taught on the blog are updated and aligned with the most innovative and cutting-edge technological advances in the field of hydrogen technologies.

The total intrinsic energy of a fuel (or of any substance) is quantified by a property known as internal energy (U). The limits on how much of the internal energy of the H2 gas can be transformed into electrical energy are established by the first and second laws of thermodynamics.

Frist Law

The first law of thermodynamics is also known as the law of conservation of energy -energy can never be created or destroyed - as expresse by the equation. The variation of Energy - mathematically d(Energy).

d(Energy)univ = d(Energy)system + d(Energy)surroundings = 0

Viewed another way, this eqution states that any changes in the energy of a system must be fully acconted for by energy transfer to the surrondings:

d(Energy) system = - d(Energy)surrondings

There are two ways that energy can be transferred between a closed system an its surroundings: via Heat (Q) or Work (W). This allows us to write the first law in its more familiar form:

dU = dQ - dW

To developed this expresion, we have substituted dU for d(Energy)system; if we choose the proper reference frame, then all energy changes in a system are manifested as internal energy changes. Note that we define positive work as work done by the system on the surronding.

We will asume that only mechanical work is done by a system. Mechanical work is accomplished by teh expansion of a system against a pressure. It is given by

(dW)mech = pdV

where p is the pressure and dV is the volume change. Considering only mechanical work, we can rewrite the expression for the internal energy changes of a system as

dU=dQ-pdV

Second law

The second law of thermodynamics introduces the concept of entropy. Entropy is determined by the number of possible microstates accessible to a system, or, in other words, the number of possible ways of configuring a system.

Except for extremely simple systems like the one in this example, it is impossible to calculate entropy exactly. Instead, a system’s entropy is usually inferred based on how heat transfer causes the entropy of the system to change. For a reversible transfer of heat at constant pressure, the entropy of a system will change as:

dS=dQrev/T

For an irreversible transfer of heat, the entropy increase will be even larger than that dictated

by last Equation

The most widely known form of the second law acknowledges that the entropy of a

system and its surroundings must increase or at least remain zero for any process:

dSuniv>=0

Thermodynamics Potentials

Based on the first and second laws of thermodynamics, we can write "rules" to specify how energy can be transferred from one form to another. These rules are called thermodynamic potentials.

• Internal Energy (U). The energy need to create a system in the absence of changes in temperature or volume. The internal energy of a system, is a funtion of entropy and volumen U=U(S,V). We can combine results from the first and the second laws of thermodynamics to arrive at an equation for internal energy that is based on the variation of two independent variables, entropy S and Volumne V.

dU=TdS - pdV

TdS represents the reversible heat transfer and pdV is the mechanical work.

• Enthalpy (H). The energy need to create a system plus the work needed to make room for it (from zero volume).

H=U+pV

Through differentiation, we can show that H is a function of S and p. H=H(S,p)

dH = dU + pdV +Vdp

dH=TdS+Vdp

• Helmholtz Free Energy (F). The energy needed to creeate a system minus the energy that you can get from the system's environment due to spontaneous heat transfer (at constant temperature)

F=U-TS

Through differentiation, we can show that F is funtion of T and V. F=F(T,V)

dF=-SdT-pdV

• Gibbs Free Energy (G). The energy needed to create a system and make room for it (from zero volume) minus the energy that you can get from the environment due to heat transfer. In other words, G represents the net energy cost for a system created at a constant environmental temperature T from a negligible initial volumen after subtracting what the environment automatically supplied

G=U-TS+pV

Though differentiation, we can show that G is fution of T and p G=G(T,p)

dG=dU-TdS-SdT+pdV+Vdp

Since we know that dU=TdS-pdV, we can see that

dG=-SdT + Vdp

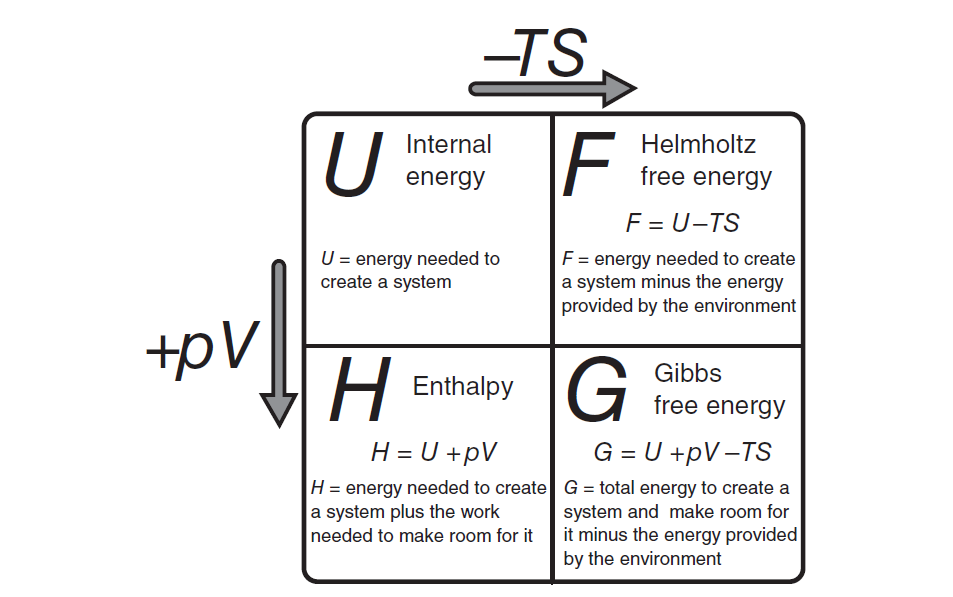
Pictorial summary of the four thermodynamic potentials. They relate to one another by offset of the "energy from the environmment" term TS and the "expansión work" term PV. Copyriht 2000 by Addison Wesley Longman.(from An introduction to Thermal Physics by Daniele V. Shoroeder)

Intrinsic quantities and extrinsic quantities

Intrinsic quantities such as temperature and pressure do not scale with the system size; extinsic quantities such as internal energy (U), entropy (S), or the rest of thermodinamics potentials such Gibbs Free Energy (G), Enthalpy (H) or Helmholtz Free Energy (F) do scale with system size.

Molar quantities such u, the internarnal energy per mole of gas) (units of Kilojoules per mole) , are intrinsic. It is often useful to calculate energy changes due to a reaction on a per-mole basis:

Δĝ rxn,Δŝrxn,Δ𝑣̂rxn

The Δ symbol denotes a change during a thermodynamic process (such as a reaction),

calculated as final state–initial state. Therefore, a negative energy change means energy is

released during a process. A negative volume change means the volume decreases during a process.

HEAT POTENCIAL OF A FUEL: ENTHALPY OF REACCTION

We will now apply what we know about thermodynamics to fuel cells. Remember, the goal of a fuel cell is to extract the internal energy from a fuel and convert it into more useful forms of energy.

What is the maximum amount of energy that we can extract from a fuel?

The maximum depends on whether we extract energy from the fuel in the form of heat or work.

As is shown in this section, the maximum heat energy that can be extracted from a fuel is given by the fuel’s enthalpy of reaction (for a constant-pressure process, dp=0).

dH=TdS

Here, dH is the same as the heat transferred in a reversible process (dQrev). For this reason, we can think of enthalpy as a mesure of the heat potential of a system under constant-presure condition. From where does this heat originate? Expressing dH in terms of dU at constant pressure provides the answer:

dH = TdS = dU+dW

From this expression, we see that the heat evolved by a reaction is due to changes in the

internal energy of the system, after accounting for any energy that goes toward work. The

internal energy change in the system is largely due to the reconfiguration of chemical bonds.

For example, burning hydrogen releases heat due to molecular bonding reconfigurations. The product water rests at a lower internal energy state than the initial hydrogen and oxygen reactants. After accounting for the energy that goes toward work, the rest of the internal energy difference is transformed into heat during the reaction.

The enthalpy change associated with a combustion reaction is called the heat of combustion. The name heat of combustion indicates the close tie between enthalpy and heat potential for constant-pressure chemical reactions. More generally, the enthalpy change associated with any chemical reaction is called the enthalpy of reaction or heat of reaction

WORK POTENTIAL OF A FUEL: GIBBS FREE ENERGY

If Gibbs free energy (G) can be considered to be the net energy required to create a system and make room for it minus the energy received from the environment due to spontaneous heat transfer, then G , represents the net energy you had to transfer to create

the system. ( the environment also transferred some energy via heat, but G substract his contribution out). In other words, the Gibbs free energy represents the exploitable energy potential, or work potential, of the system.

Relationship between Gibbs Free Energy and Electrical Work

For a fuel cells we are specifically interested in electrical work, so What is the maximum amount of electrical work that we can extract from a fuel cell reaction?

As we have done previously, we define the variation of G (mathematically dG) as:

dG = dU - TdS -SdT +pdV +Vdp

We can insert the expression for dU based on the first law of thermodynamics into the vatiation of G. However, this time we expeand the work term in dU to include both mechanical work and electrical work:

dU=TdS - dW=TdS - (pdV +dWelec)

which yieds

dG=-SdT + Vdp -dWelec

For a constant-temperature, constant-pressure process (dT, dp=0) this reduces to

dG=-dWelec

Thus, the maximum electrical work that a system can perform in a constant-temperature, constant-pressure process is given by the negative of the Gibbs free-energy difference for

the process. For a reaction using molar quantities, this equation can be written as

Welec = −Δgrxn

Remember that the constant-temperature, constant-presure assumption used here is not really as restrictive as it seems. The only limitation is that the temperature and presure do not vary durign the reaction process. So It is important to realize that the expression derived above is valid for differents values of temperature and pressure as long as these values are not changing during the reaction.

Relationship between Gibbs Free Energy and Reaction Spontaneity

In addition to determining the maximum amount fo electrical work that can be extrated from a reaction, the Gibbs free energy is also useful in determining the spontaneity of a reaction. Obviously, if ΔG is zero, then no electrical work can be extracted from a reaction. Worse yet, if ΔG is greater than Zero, the work must be input for a reaction to occur. Therefore, the sign of ΔG indicates whether or not reaction is spontaneous:

ΔG > 0 Nonspontaneous (energetically unfavorable)

ΔG = 0 Equilibrium

ΔG < 0 Spontaneous (energetically favorable)

A spontaneous reaction is energetically favorable; it is a "downhill" proces. Although spontaneous reactions are energetically favorable, spontaneity is no guarantee that a reacction will occur, nor does it indecate how fast a reaction will occur. Many spontaneous reactions do not occur because they are impeded by kinetic barriers. Fuell cells, too, are constrained by kinetics. The rate at which electricity can be produced from a fuel cell is limited by several kinetic phenomena.

Relationship between Gibbs Free Energy and Voltage

The potential of a system to perform electrical work is measured by voltage (also called electrical potential). The electrical work done by moving a charque Q, mesured in colombs, through an electrical potential difference E in volts is

Welec = EQ

if the charge is assumed to be carried by electrons, then

Q = nF

where n is number of moles of electrons transferred and F is Faraday's constant (96.485 C/mol). So Combining above ecuations,

Δ̂g = −nFE

In a Hydrogen-Oxiden fuel cell

H2 + 1/2O2 ⇌ H2O

has a Gibbs free-energy change of -237kJ/mol uder standard-sate conditions for liquid water product. The reversible voltage generated by a hydrogen - Oxygen fuel cell under standar-state conditions is thus

Eº = - Δ̂g /(nF)

-237000 J/mol / ( 2 mol e-/mol reactant * 96485 C/mol) = 1.23 V

At Standar-satate conditions, thermodynamics dictates that the highest voltage attainable from H2-02 fuel cell is 1.23 V. To get 10 V from fuel cells, we usually have to stack serveral cells together in series.

PREDICTING REVERSIBLE VOLTAGE OF A FUEL CELL UNDER NON-STANDARD-STATA CONDITIONS

Standard-state reversible fuel cell voltages (Eº values) are only useful standard-state conditions (room temperature, atmospheric pressure, unit activities of all species). Fuel cells are frequently operated under conditions that vary greatly from the standard state. For example, high-temperature fuel cells operate at 700 - 100 ºC, automotive fuel cells often operate under 3-5 atm of pressure, and almost all fuel cells cope with variations in the concentration (and therefore activity) or reactant species.

Reversible voltage variation with Temperature.

To understand how the reversible voltage varies with temperature, we need to go back to our original differential expression for the Gibbs free energy, from which we can wirte (for molar reaction quantities):

(d(Δĝ)/dT)p=Δŝ

We have previously shown that the Gibbs free energy is related to the reversible cell voltage by Δ̂g = −nFE. Comobining both ecuations allows us to express how the reversible cell voltage varies as a funtion of temperature

(dE/dT)p=Δŝ/nF

We define ET as the reversible cell votage at an arbitrary temperature T. At constant pressure, as:

ET = Eº + Δŝ/(nF)*(T-T0)

For example, in a H2-02 fuell cell. Δ̂srxn = −44.34 J/(mol⋅K) (for H2O(g) as product). The variation of cell voltage with temperature is approximated as

ET = Eº − (2.298 × 10−4V∕K)*(T-T0)

Reversible voltage versus temperature for electrochemical oxidation of a variety of fuels.

(After Broeres and Ketelaar)